Computational modelling of adolescent decision making

How does reward processing and control inhibition change throughout adolescence?

Abstract

The computational modelling of decision making tasksis a powerful method in identifying complex cognitive pro-cesses that can be used to create a more detailed pictureof the underlying learning mechanisms. In this work, weshow how the combination of biases and sensitivity to re-inforcements are reliable predictors of behavior in a decision-making paradigm. We present a Bayesian hierarchical computational models which attempt to capture increasingly more complex learning mechanisms on the Passive Avoidance Learning Paradigm (PALP) task, using a reinforcement learning framework. Model selection is doneon the basis of predictive accuracy, leave-one-out cross-validation, and Bayes factor. We illustrate the usefulness ofthe selected model through the identification of developmen-tal changes in subpopulations, and how these can be usedfor classification. We identify strong developmental changesin action bias and sensitivity to reward in adolescents, fromages 12-13 to 17 years old. Furthermore, a group of highrisk cannabis users were compared to con-trols and differences in sensitivity to punishment and actionbias were identified. In this work, we’ve successfully distinguished developmental changes which can be used to assessdivergent maturation trajectories. The significance of thesefindings extends to the design of new standards of cognitive maturity that could lead to better diagnoses of mentalhealth disorders, such as depression and addiction.

Accepted poster presentation, SOBP 2020 (online)

In order to model the choice made during the task, we need to assign a probability distribution over the space of possible actions. For the PALP case, there are only two possible actions, go or no-go, which can be formulated as originating from a Bernoulli distribution after making some simplifying assumptions, such as independence between trials. Moving forward, we define the probability that the player will select the go action as:

$$P(y_{it}=1|\alpha_{i},\beta_{i},\phi_{ir},\phi_{ip}) = Bernoulli(P_{Go_{t}})$$

where each parameter is defined below: - N: number of players
- T: number of trials per player
- i: player index, i in 1,2,...,N
- t: time index, t in 1,2,...,T
- y_ij: player i choice at trial t
- P(Go_t): probability of picking the go action at time t

Now we can see how the probability of either action is a function of player cognitive attributes. This approach allows us to estimate the parameters, and estimate likely values from human observations. Below you can see a brief description of their role in our decision-making model:

We had a sample of N=500 players of around 12 years of age at the first year, up to 17 years old after a 5 year follow-up. The posterior distributions of the parameters as defined in Table 1 are plotted grouped by year:

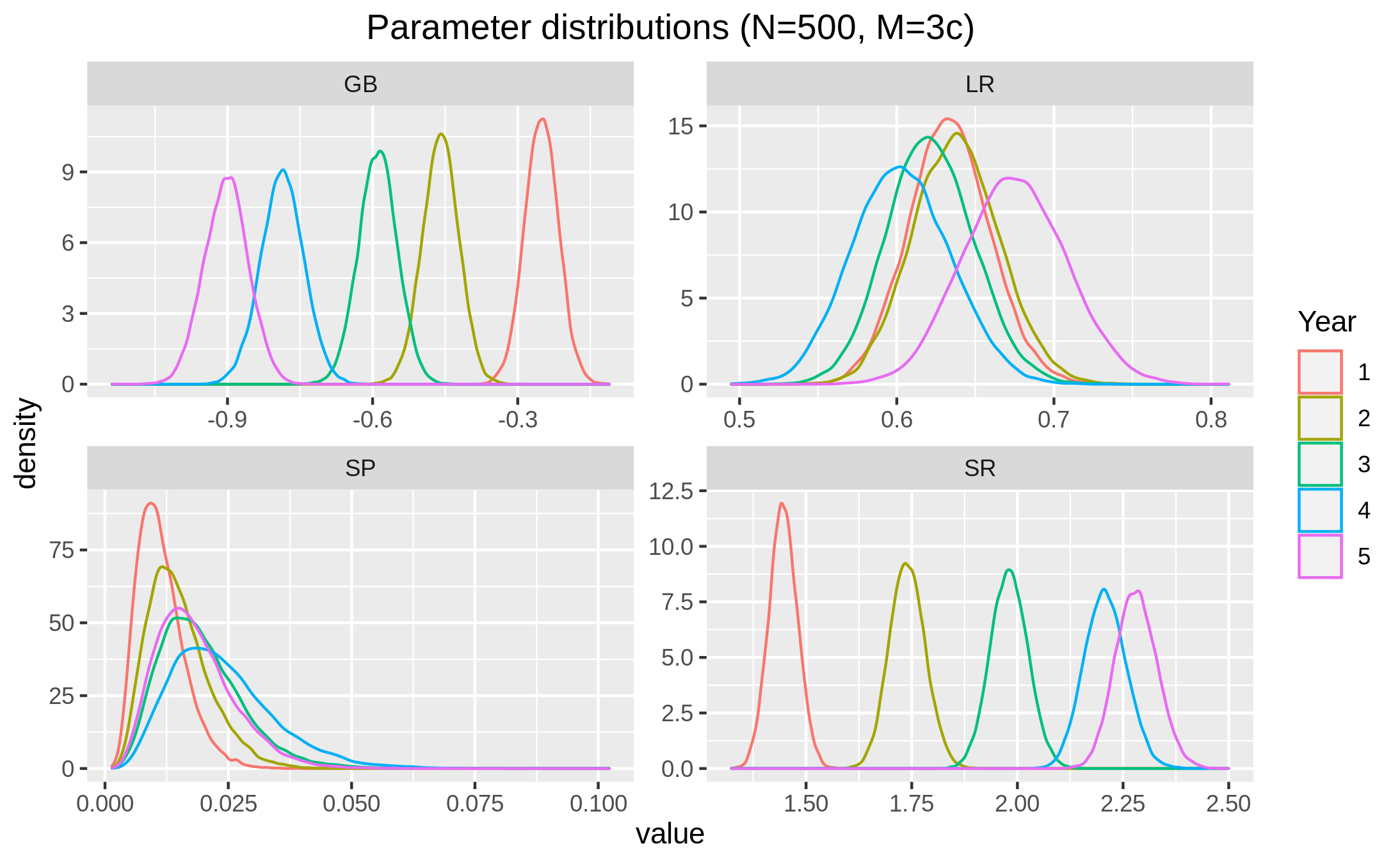
Of notable interest is the inverse relationship between the (Go) bias term (GB) and the sensitivity to reward (SR). The increase in sensitivity to reward through adolescence, while response inhibition increases, is a trademark for the maturity gap. Using these kinds of models allow us to relate observed decision making to cognitive processes, and track their development, or maybe help identify injuries by establishing new metrics using these cognitive profiles. In addition to that, the strong developmental trends suggest that this approach could be used in developping new measures of maturity, and moving away from arbitrary cutoffs e.g. 18 y.o. is considered an adult by law here in Quebec. Are all 18 year olds adults?